تحميل نماذج امثلة عن الدوال الخطية

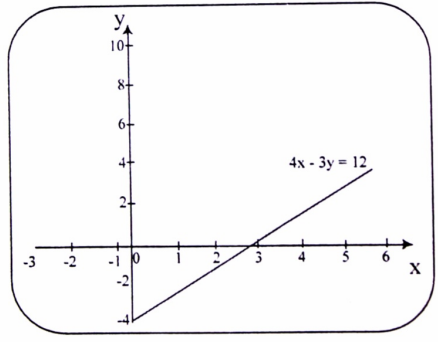
يوجد في الرياضيات الكثير من المعادلات، والتي منها الدالة الخطية هي الدالة الرياضية التي تنشىء خطًا مستقيمًا عند رسمها بيانيًا، ويرغب الكثير بالحصول على نماذج امثلة عن الدوال الخطية لكي يتم التدريب عليها بشكل جيد، حيث تعتبر من الدوال التي لها أهمية كبيرة في الرياضيات.

نماذج امثلة عن الدوال الخطية

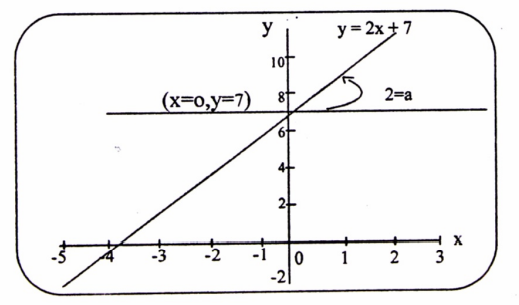
تعتبر الدالة الخط هي دالة رياضية تنشىء من خلال خط مستقيم عند رسمها بشكل بياني وتمثل جبريًا y = mx+b، ويمكن أن يتم وصفها بالكثير من الصيغ مثل مستقيم في المستوى الدريكارتي ثنائي الأبعاد أو ثلاثي الأبعاد، وبهذا تسمى دالة خطية وهي دالة ذات متغيرات وثوابت ولكن ليس لها قيمة أس ويمكنك التعرف على أمثلة عن الدوال الخطية “من هنا“.

دالة خطية

تعتبر الدالة الخطية هي التي يكون رسمها البياني خطيًا بهذا تكون دالة خطية، وهي تعتبر متعددة الحدود من الدرجة الأولى وتربط الدالة الخطية المتغير التابع بالمتغير المستقل من خلال علاقة خطية الشكل القياسي لتمثيل الدالة والتي هي ي = ف(س) = م س + ج على أن يكون y هو المتغير التابع، و x هو المتغير المستقل، x م هو معامل و ج هي القيمة الثابتة.

دالة غير خطية

الدالة غير الخطية هي الدالة التي ليست خطية بطبيعتها، أي أن بها فجوة وهي لا تمثل الخط المستقيم، ويمثل الرسم البياني لهذه الدوال الدائرة والقطع المكافئ والقطع الزائد وغيرها، وتسمى هذه الدوال بالدوال التربيعية والدوال المكافئة والدالة الزائدة وغيرها.

صيغة الدالة الخطية

يتم استخدام صيغة الدالة الخطية من أجل تمثيل الهدف لمسائل البرمجة الخطية، وهذا يساعد على تعظيم الأرباح أو تقليل تكلفة المدخلات والبيانات وهي دالة خطية بشكل عام، قد تكون الدالة الخطية في LPP المقدمة في والغرض من مسائل البرمجة الخطية هو f(x) = ax + b وتقليل الدالة الخطية في ظل بعض الظروف والموردة.

خواص الدوال الخطية

هناك ثلاث معايير تعبر عن الدالة الخطية بشكل عام وهذا لأنها تختلف عن غيرها من الدوال الرياضية الأخرى، فهي يوجد بها متغيرين فقط وجميع القوى التي توجد بها من الدرجة الأولى، وينتج عنها رسم بياني بخط مستقيم وفيما يأتي نتعرف على أبرز خواص الدوال الخطية:

1- الرسم البياني خط مستقيم

تعتبر جميع نقاط الأزواج المرتبة التي تجعل الدالة الخطية صحيحة خطاً مستقيماً في الرسم البياني، ويمكن وصف الدالة الخطية في هذه الحالة من خلال متغيرين كعلاقة خطية بين س و ص وهذا يعنى متغيرين تعتمد قيمة أحدهما ص على الآخر س ( لكل قيمة س هناك قيمة واحدة مقابلة لـ ص )، وبالتالي يكون س هو المتغير المستقل في هذه الحالة ويتم رسمه على طول المحور الأفقي و ص هو المتغير التابع.

2- ميل الدالة الخطية

يعتبر معدل تغير الدالة الخطية بالمنحدر أو الميل وعادة ما يتم تمثيله بحرف م هو ميل الدالى الخطية، وهو عبارة عن نسبة التغير الرأسي بين نقطتين إلى نسبة التغير الأفقي وبين نفس النقطتين س1 و ص1 وتمثل النقطة الأولى و(س2، وص2) تمثل النقطة الثانية، ويتم توضيحها رياضيًا م = (ص2 – ص1) / (س2 – س1).

3- التزايد والتناقص والثابت للدالة الخطية

يتم تحديد ما إذا كانت الدالة الخطية متزايدة أو متناقصة أو ثابته من خلال الميل في الرسم البياني، حيث تكون الدالة المتزايدة بها ميل موجب م >0، والخط المستقيم الناتج يميل إلى الأعلى من جهة اليسار إلى اليمين والعكس في الدالة المتناقصة، وبالنسبة إلى الدالة الثابتة يكون ميلها 0 ويكون الخط المستقيم لها بشكل أفقي.

يتم استخدام الدالة الخطية في حل الكثير من المشكلات المختلفة التي يتعرض لها الإنسان في الحياة اليومية، ولهذا فهي من التطبيقات المهمة التي يجب أن يتعلمها الأطفال وهم في سن صغير لكي يكونوا قادرين على تطبيقها بعد ذلك.